big o

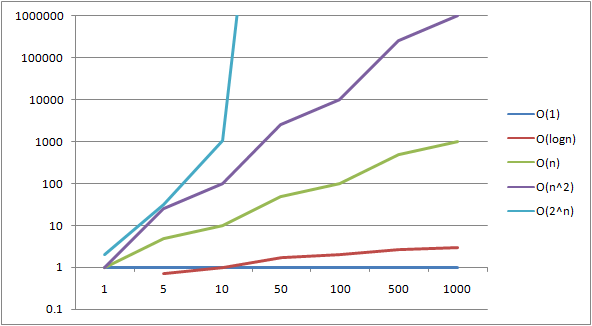
Big O notation is used to classify algorithms by how their runtime changes relative to the input, as the input grows arbitrarily large. Runtime is defined by time and space complexity.

Below are some common run times:

  • O(1): a constant-time method
    • the algorithm will always execute in the same time regardless of its input size.
  • O(N): a linear-time method
    • the algorithm will grow linearly with its input size
  • O(N^2): a quadratic-time method
    • the algorithm will execute proportional to the square of the size of its input data
    • nested iterations will be O(N^3) or O(N^4)
  • O(2^N): exponential-time method
    • execution time will double with each additional element in the input data
  • O(log N): logarithmic-time method
    • I like this example from stackoverflow
      • Given a person’s name, find the phone number by picking a random point about halfway through the part of the book you haven’t searched yet, then checking to see whether the person’s name is at that point. Then repeat the process about halfway through the part of the book where the person’s name lies. (This is a binary search for a person’s name.)

Example I’m told that a common interview question involves checking if a number is a part of the Fibonacci sequence. There are many ways to implement this method, but ideally we’d want to implement Fibonacci in the most efficient way. A common complaint about writing a solution recursively is its high runtime. Using 3 examples below:

Write a method to check if a number is a part of the Fibonacci sequence.

Pseudocode

  • Input: a number
  • Output: a method to check if that number is part of the fibonacci sequence arr. Return true or false
  • Fibonacci numbers: [0,1,1,2,3,5,8,13,21,34,55,89,144]
  • each number is the sum of the previous 2
  • start with [0,1] as the first 2 numbers
  • f(n+1) = f(n) + f(n-1)

Solution A - iterative

def fibonacci_iterative(n)
  array =[0,1]
  2.upto(n) do |num|
    array << (array[num-2] + array[num-1])
  end
  array[n]
end

Big O: O(n)

Solution B - recursive

def fibonacci_recursive(n)
  return n if [0,1].include? n
  fibonacci_recursive(n-2) + fibonacci_recursive(n-1)
end

Big O: O(2^n)

References: